Multiplication Strategies Part 1

I've had several parents ask for some assistance helping their kids learn multiplication and division. They don't want another video, worksheet, or app. They just want someone to sit down with them and help them develop strategies for helping their children learn their facts. Are you among them? I'm compiling a list of helps here. I'll add to it as time goes on.

The first thing I always tell parents is that I believe some people aren't really capable of memorizing facts. I know this sounds like I'm saying they can't learn, it's is not the same thing I promise. But rote memorization really truly does not work for some people and has been the cause of frustration in the mathematics classroom for years. I have a firm belief that some math students will need to develop strategies and habits, which will help them retrieve information stored in their brain. This might include using fingers, counting objects in the room, or visualizing dots in their minds. Guess what? Their math teachers and tutors at times count on their fingers, look at concrete objects, and/or visualize patterns to solve problems as well!

1. Use the distributive Property.

The distributive property is one of the basic laws of how numbers work with each other. It works with both addition and multiplication, and helps students break down larger facts into more bite-sized facts that are easier to solve. The reason this strategy works well is it is not a trick, it's a law of numbers. It helps math students break apart numbers and use their values to find related facts they've already memorized or effectively stored for retrieval. The distributive property of multiplication basically states that numbers can be spread out to be multiplied and added to make an operation easier to solve.

Here is an example. Let's multiply 3 x 6. I'm starting off with a seemingly simple fact so it's easy to see how this works.


My student says, "Miss Stefany, I don't know my sixes!"
"Ok, what about your threes?"
My student, "No, I don't know my threes either!"
"No problem, do you remember how to count by 2s?"
My student, "Yes, 2, 4, 6, 8..."
"Perfect!"

Now you're asking, "How on earth is counting by 2s going to help me multiply 3 and 6?"
For that answer we need to go back to our basic addition facts. 6 is equal 2 + 4, correct? The distributive property of multiplication tells us that if 2+4=6 then 3x6=(3x2)+(3x4).


If you count the blocks in the diagram, you'll see that it works. There are 18 blocks in the 3 by 6 grid and there are 18 blocks in the 3 by 2 and 3 by 4 grid as well!

Maybe your student doesn't know his fours yet either. No problem, just break it down a further step. If 6=2+4 it also equals 2+2+2. So 3x6 also equals (3x2)+(3+2)+(3x2).


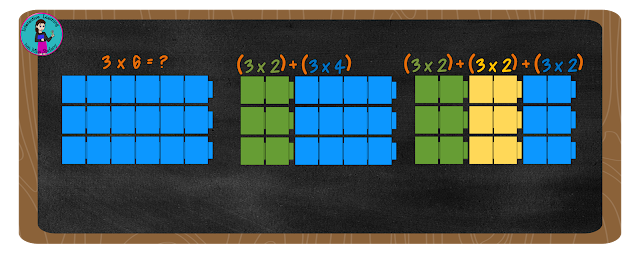
Again, counting the blocks shows that it works! And I can assure you, it works every time, no matter what the numbers are or how big they are.

You can also break the numbers down into any of their equal parts.
For example, 6=1+5, so 3x6=(3x1)+(3x5)
                      6=3+3, so 3x6=(3x3)+(3x3)

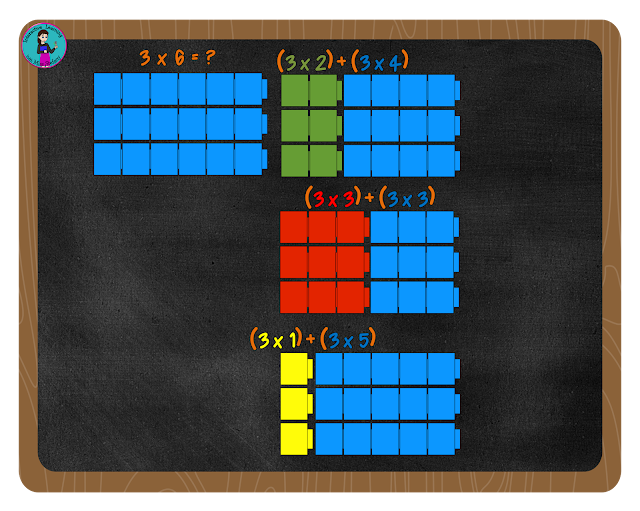
Just a tidbit here. If you your child was among those learning all the partners of numbers over the past 3 years with their Common Core Curriculum, and you couldn't figure out what they would ever do with that. Here it is! Be thankful they spent so much time with that concept, because now this will make so much more sense. If your child wasn't one of the students drilled on this skill, then see this post here for more information that might make using this strategy a little more clear.

Would you like to try some multiplication problems using this strategy with answer guide to check your work? Here's a freebie just for parents!

Common Core Haters, You Really Should do Your Homework!

***DISCLAIMER*** This blogger in no way endorses, supports, or advocates for Common Core State Standards, or any other federal or state legislation that robs educators of their autonomy in the classroom!

This news report just came across the virtual desks of a group of fellow teachers. We hashed it out, and came to the realization that this news reporter doesn't know 1) a thing about these standards, and 2) what is involved in the "old way" of doing simple math problems, and 3) how this strategy works.

How many times have you seen a video like this over the past 6 years?



I see two faulty lines of reasoning in this example which leads me to believe these opinion pieces are not meant to inform the public nor are they produced with the kids in mind. They are just simply haters who are gonna hate, no matter what the cause. And to be honest, I think it makes everyone who jumps on their bandwagon look like a bunch of numbskulls!

First, this guy (news reporter, NOT teacher) doesn't use an example that makes sense. Those of us teaching second graders this strategy are NOT using examples that DON'T require regrouping or higher order thinking. It is a strategy to apply in those exact situations. Second, just like all of the other CCSS haters out there, he oversimplifies the old school way.

Note to haters and hater lovers: It's only as simple as you make it because your K-2 teachers labored for hours to help you "get it" the way you got it! And chances are, your parents were complaining to anyone who would listen that this "new way" of doing math was ridiculous and should be thrown out of the schools.

Here's the real background to all that "simple subtraction" when using a subtrahend that requires regrouping:

Step 1 involves at least 3 other steps. Sure when you are using numbers like 23-3 you can eliminate those extra steps, but problem is, most of the problems our students will come up against later in life won't be that simple! What's more, when we tell them over and over again for 3-5 years that you can't take 5 from 3, it confuses them when they start working with negative numbers. Not only does this way bog down the processing power of our students, it also creates false mathematical reasoning that comes back to bite them in a few short years.



Instead, we start by teaching math partners, grouping in 5s and 10s. Students learn to quickly recognize partners of 5 and 10, this starts the same time they are learning to count to these numbers, so it's natural. Then we teach them to add, and that subtraction and addition are intrinsically connected (ok, maybe not that term). But they learn number bonds rather than addition/subtraction facts, helping them automate the fact families 2+3=5, 3+2=5, 5-3=2, 5-2=3. Then we teach them about place value, that 10 ones can be grouped to make 1 ten, and so-on. All of this groundwork is laid BEFORE problems like this are introduced.

Compare that "old way" to the real thought process of the "new" and "overly complicated way": 

Now our student sees this problem in all of its component parts. They are quick to find partners of 5 and ten, and they've developed mental math strategies that help them build up (the natural counting order) rather than count back (and get stumbled over 13, 12, 13). Just as in the case of the old way, most of this thought process isn't written out, it takes place in the competent mind of a young learner.

The question here isn't whether one way is more difficult, or even developmentally appropriate. It's which method lays a better framework for future maths. What is the purpose of K-2? Isn't it to help students develop the fundamental skills of reading and computing so they can tackle the more challenging content that will be thrown at them for the next 10 years? Decomposing numbers, using ten partners, and looking at subtraction problems as missing addend problems may be new ways of teaching fundamentals to second graders, but it's not "new math." The numbers still all follow the same rules as work together the same as they always have, no legislation has the authority to change that!

Here's a look at that first problem the news reported attempted to explain. First, there is no need to break this problem down once you've separated the tens and ones. This "new math" looks like this:

Looks pretty simple, doesn't it? 

No, this doesn't do this justice, let me see the examples that require regrouping to solve, side-by-side. And while we're looking at these, think about 2 things. 1) which one will cause less frustration in the middle grades when kids are going crazy with hormonal changes and life is just starting to get real? 2) which one requires the student to memorize less steps, thus freeing up valuable processing space for solving real life problems? AKA which skill transfers better into the real world of buying groceries and paying taxes?

 

And I just have to clarify, if the news reporter would have done his homework to learn how to use this strategy, and still chose the same problem, it would have looked like this: 

Final thoughts: News reporters, parents, and even concerned citizens, if you are going to complain, berate, and deride a way of teaching something, please, PLEASE do your homework! Stop making yourselves look like fools. When you jump on an emotionally charged bandwagon and retweet and hashtag everything you see that is against the same issue, without scrutinizing it, you are just giving the case into the hands of those you oppose! 

Dear teachers, tutors, and other educators, help me get the word out, pin, share, like, tweet, and repost (with a link back please) to help inform these poor uninformed haters! ;)

Teaching Math as a Second Language

I've had a dry spell here on the blog, so I want to start with, "Hey! How ya doin'? It's been a while!"

Today was a great day, I had 0 regularly scheduled students, and 3 reschedules. These days are great because there's really no rhyme or reason, and I get to learn a lot about myself. I started with an Algebra student, then went to work with 2 second graders (1 math and reading and the other just math).

I was reminded today about an old project that has been sitting in the dusty back edges of my "some day I will get to this" files. Ages ago, when I was in my 3rd year of college, I took a Teaching English Language Learners course. It was really a "for fun" course for me. There isn't a real need in my area, and I'm not fluent in any other language. I was just curious. I LOVED the course. There were so many valuable tidbits that I could see myself applying to so many areas of teaching English speaking students.

Of course, you well know that math is my thing. And I've heard time and time again, people crying, "I just don't understand!" It was the same cry I was hearing ELLs bemoaning! It hit me that Math is truly a completely unique language. Sure there are words that sound like everyday language, but they usually have a different meaning or application. I found, through some blind studies with my children, that understanding the vocabulary was a determining factor to understanding content.

Ok, now I have to shamelessly admit something here. I thought that this was a brilliant construct of my own, that no one else on Earth had thought of this, made this connection. Unfortunately, I cannot take the credit. While, yes, in my mind, it's all mine. I did some research that landed me on the page of a teacher, Herb Gross. I haven't done a ton of research into his philosophy and methods, but from what I've read, we'd have a lot of fun teaching math together. Herb, if you are out there reading this and ever find yourself in Michigan, look me up!

The basic idea is that as teachers we take a step back from the math curriculum, whether it's 9th grade Algebra or 2nd grade skip counting, and we look at it through the eyes of someone who doesn't speak the language. Rather than teach them "how" to solve a problem, we help our students understand "why" the solution works. Instead of using algorithms and formulas as our backbone of instruction, we use vocabulary and language development.

How does this look? 

The first rule is to front load vocabulary and key terms. I'll use the Algebra student I was working with today as an example. We've been working together for a few months, and I noticed right away that he didn't speak Mathenese ( I promise I didn't make that word up! See this search for proof:). I started each lesson with a moment to collect our thoughts and think about what we already knew about the key words. Sometimes it was nothing, sometimes it was a related word in science. For example, when we discussed dependent and independent variables he quickly remembered that a dependent variable was something that would be caused by something else, and that something else was an independent. Activating this prior knowledge, and connecting his science notes with his math lesson helped him to make sense of the entire lesson. 

The second rule is to infuse your lessons with visual aids.

A strategy borrowed from Teaching English Language Learners, providing visual aids helps our students process the information in a spatial way. They can connect colors and shapes to verbal cues. These visual aids can be 3-dimensional manipulatives, anchor charts, posters, charts, diagrams, or simple little drawings. I find that it is most beneficial to get  the students involved in creating these visual aids. After I've provided a cue I give them an opportunity to develop their own, and then we analyze their developments. This entire process not only helps each student develop understanding of the concepts, but also cements a learning strategy they can take with them on their life long learning journey!

The third rule is to use your student's native language as often as possible. I know this sounds a little strange when we are talking about teaching math to a student who speaks the same language as us. However, if my student is particularly interested in science, or quickly refers to science terms, I use that, and try to make those connections as soon as possible and as often as possible. A few years ago I was working with a 10th grade Geometry student who saw absolutely no need for math. This particular student had plans to be an artist, and was convinced math couldn't help her. When we started discussing perspectives in drawings and angles of lighting, I was able to see a light bulb glow for her. Immediately, everything we had discussed about adjacent angles of a triangle, and angles of elevation became crystal clear to her. Learners will naturally make connections to contexts they have a high interest in, so use it!

Ok, I think I've kept you long enough. I'll save some more of this for another post later. Here's to helping our students develop their Mathenese!

By the way, I'm developing an interactive notebook type of vocabulary journal for my 9th grade Algebra students, If that's something you'd be interested in, head over to my store and pre-order your copy. I promise to have at least a unit complete by the end of the month, and I'll keep adding to it throughout the year. As with all of my growing units, the sooner you you grab it the less it will cost ;) Here's just a little snippet of the first few pages.

Lesson Deli Hop: Don't do this, instead try this!

For years I've been seeing these "getting to know you/me" worksheet/scrap book pages for the first day/week of school. They are fun, and the kids really love to tell everyone about themselves. But I just don't really understand why they are so big. I guess that's one difference between a classroom teacher and a private tutor. We get to know our students on different levels.

My first priority, when working with a new student, is to discover the most I can about their unique skills and abilities right away. This really helps me cater our lessons to their exact needs, which is often very different from one student to the next, even when we're working on the same or similar concepts. This is one area I sincerely tip my hat to all of you classroom teachers out there!

Part of my intake process included a Multiple Intelligences survey. I downloaded a free copy from a trusted source, and have used it for more than 2 years. It helps to a degree, but really wasn't enough for my purposes. So I got to work ;)

This spring and summer I've been fine tuning my survey to include goal setting and intelligence building ideas. I've even added a PowerPoint Presentation to use as a teaching tool, so students aren't only helping me get to know them, but they are learning more about themselves and how they learn. It's exciting to the student and their parent realize why some things have been so difficult for so long and why some things just come so easily. 

So, now I'm ready to share this with the world of teachers out there. Here's a new and improved way to get to know your students in the first day/week of school. You'll know a lot more than their favorite food and where they vacationed over the summer. Now you will know who is who in the classroom, and this will help you plan your lessons all year, to really meet the needs of your students. 

Here's what it looks like:

1. PowerPoint Presentation

2. Posters

3. Student Booklets (covers for girls and boys, and I"m working on an older version right now)

4. Intelligence Catchers (and some other fun and interactive skill building activities)

5. Teaching guide. (sorry, I don't have a pic, but you get the idea ;) )

For this hop, I pulled out the posters and made them half pages so you can get a peek at this workshop. Enjoy!

If you would like to win this workshop and $10 credit in my store, leave a comment on this post, and tell me how you plan to get to know your students this year! I will chose 1 winner on Monday, August 17th.

Oh, and don't forget to click through to the next back to school tip, from my friend Neetu at Cinnamon's Synonyms!

Tutors Love Back to School

It's that time of year again, already! I don't know about you, but my summer has gone by far too quickly. The sitewide Back To School sale at Teacherspayteachers is already upon us, which means teachers everywhere are loading their carts and preparing their classrooms. What about the tutors out there?

Yes, we have some back to school preparation to do as well. Whether you've been tutoring for years or just starting out this year, you'll be happy you landed on this little linky! Several other tutors and I have dusted the cobwebs from our thinking tanks, and put together our best tips for back to school that will help tutors the most. 

When I hear "back to school," aside from SHOPPING, the first thing I think about is meeting new faces. My first session with students always involves getting to know them. Our next step is planning. We set goals, plan our first few lessons, and get to work. I truly believe that when a student sets their own goals and writes out their own plans to achieve them, they are better positioned to succeed.

This year, make it a point to work with your students, setting goals, making plans, and keeping track of progress. Put the pen in your students' hands, and let him/her take accountability for their efforts. You'll be happy you did!

I pulled a couple pages from my student planner packet to give you a sneak peek at what's inside. Feel free to use these with your students this back-to-school season!

Here's the whole thing...Calendar, weekly planning pages, To-Do Lists, Graphic organizers to help plan out big projects, Resource reference sheets for math and writing. Want to hear the best part? This is a growing resource. That means I'm going to keep adding to it as I come across elements and ideas that will help our students even more! During the sale you can grab your copy for 28% off the regular price (Don't forget to enter the code BTS15 when you check out!).

For more tips from Tutors and special deals this back-to-school season, click on below!

An InLinkz Link-up

Swap, Share, Give- Tutors on TPT Blog Hop

Over the past couple of weeks, I've been working with a few other TeachersPayTeachers authors who are also tutors. We've swapped resources and used them with our own students, I am happy to say that I get to share with you a helpful little resource, from Catia Dias. If you haven't checkout her shop before, click her logo below to see some of the fantastic resources she offers.

The resources I chose, was her Place Value Bell Ringers. 

These have an obvious application in the classroom, but I wondered how a tutor could use them. As I thought of one of my students I soon realized a quick and easy way to use these short and simple worksheets to get their minds engaged right away! I think other teachers might find this adaptation helpful as well. 

 

I cut apart the pages into three strips, this particular student is very easily overwhelmed, so I usually use a task card-like system rather than worksheets. He easily found where all of the values belonged without a lot of reminding. Then I added the review of partial products.

This wasn't our initial instruction on partial products. The week prior was his first experience with this concept of multi-digit multiplication in school. He was so flustered with his homework and lack of understanding that it was difficult to help him make sense of it.  Using these short and simple place value practices to get his mind engaged, thinking about the value of each digit, really helped the concept of partial products to find its way into his working memory!

I have another younger student, she's just starting to add to multiples of ten, who I think will benefit from these as well. I'll be working with her next week, and I can't wait to see how her session goes!

These images above show the slips from Catia's resource in a personal wipe-off board I use with all of my students. (sorry for the glare, I haven't found that "right angle" to avoid it!) You can find out how to make your own wipe off boards HERE

Catia Has been reviewing my Simplifying Fractions & Improper Fractions Anchor Charts w/Quick Worksheets If you'd like a sneak peek at those anchor charts, just click the image below to get a free copy!

(Click here to see Catia's Review of My Simplifying Fractions Packet)

And here are the other tutor-authors who participated in this swap, check out their swaps, and grab their freebies!

An InLinkz Link-up

Laminate double-sided Playing Cards

This might not be new to you, but when I first figured it out, I was blown away! Do you like to print cards and other center pieces double-sided, but then have trouble laminating the pieces? I did. I'd glue the backs to the fronts, cut them out, then the slip-n-slide would begin. Well, I don't play that game anymore, and now you don't have to either.

Here are the Match Up Style games currently in my store:

This one is a Freebie! And still bares my old store name ;)

Thanks again for stopping by. Please leave a comment below to let me know what skills you'd like to see on a Match Up Card Game!

Test Prep Blog Hop: Students Teach

Welcome to another blog hop brought to you by the teacher/authors of The Lesson Deli!

I don't think it really matters what part of the country (if you live in the US), you've been "unseasonably cold" these past few weeks. My friends at the Lesson Deli and I decided we'd do our best to help you warm up a bit, with a Starbucks Gift Card giveaway. Don't miss the link at the end of this post!

Teachers, it's that time of year again. Test Prep Season. Most of us would love to forget about it, but we can't. Even my fellow tutors and I feel it. It's not bad enough that we're feeling the February blues, but we have to get our learners ready for the next round. What do you do? Do you have some tried and true test-prep strategies, resources, or routines?

I'm from the school of thought that the best way to learn something is to teach it. When I have a student who needs help preparing for a test, I have him teach the material to me. Sometimes he's confident, sometimes she's nervous, most of the time they are excited to have the floor. I hand over my Expo Marker, and sit down with a notebook. 

As my student teaches me how to conjugate a verb, convert a fraction, or set up an equation, I take note of whether he's using the specific vocabulary that will be on the test. I make a note of how many times she says "um" or "like" as an indicator of how comfortable she is with the material. One thing I do not do is interrupt. Even if she is wrong, or even if he will end up at an incorrect conclusion. 

Many times, by the time s/he gets to the end, s/he's figured out their own mistake and can go back and correct it. Whether the conclusion is correct or way off base, I ask, "Does your answer make sense?" "Or, is there another way you could have done that?" That is usually all it takes for the student to look back over the work and find a mistake or two. 

How can you duplicate this teaching back process in the classroom? Small groups is one way. Each group will focus on one skill or concept, and the participants take turns teaching to their classmates. Participants use this free rubric to rate each "teacher's" lesson. (I include this rubric in my 6th grade Math skills Task Cards. The task cards offer a test-like question, then direct the student to show how they know, or explain why it works.)

In honor of the recent Teachers are Heroes TpT  sale, I thought I'd keep the love going with a $15.00 gift card to my favorite store. There are several ways to enter in the rafflecopter below. Best wishes!

a Rafflecopter giveaway

And here is the next Lesson Deli teacher/author, with another tip to help you through this testing season: 

Make sure to click through until you reach the Lesson Deli Blog so you can enter for your chance to win the Starbucks gift card, AND a bundle of test prep goodies from all of us involved in this hop. Happy test-prep season!

My Teacher Hero

We all have at least one. That one great teacher who changed everything, encouraged us, or just finally helped us "get it". Mine was a phenomenal middle school teacher. I've written about her before, but I guess it never gets old.

Mrs. Turner... When I saw that name on my 6th grade course list, I freaked out. I knew a couple of 7th graders, and they all told me, "Just hope you don't get Mrs. Turner for English!"  "She's mean. Nasty," they all said. "She once threw a chair across the room!" they warned me. "She loves to give Es" they said.

I was so scared. I loved to read, and writing was a favorite pastime. But I wasn't spectacular at either of them. Having this hard, cruel, hot-tempered teacher had me shaking in my high tops! All of that would ease in only a few weeks.

Yes, Mrs. Turner was strict, and she didn't sugar coat things. But she wasn't hot tempered. She just didn't take the bull that inner city kids tend to give their middle school teachers ;) And I wasn't one of those kids anyway!

Her class was hard...Brutal to be honest. I didn't do well, at all. But Mrs. Turner must have seen something in me that I didn't. She asked me to stay in her room some lunch periods so we could work on skills. We conjugated Hundreds of verbs a few times after school. No one ever asked her to do this. She just offered.

I ended up with her my 7th grade year too, and this time, I jumped up and squealed when I saw her name on my slip! I was so happy to have such a caring teacher, that wouldn't let the trouble makers ruin the class for the rest of us. It didn't hurt that she happened to group me with a "weird heavy metal girl" that first year, who had since become my best friend :D.

Besides the help and attention she gave the shy, out of place, white girl, I remember another touching thing about Mrs. Turner. It seemed that every week she would get a visitor (OK, maybe not every week, but at least twice a month). Some times they were older teenagers, sometimes young adults, and a few times they were older adults (Mrs. Turner wasn't "old" but she wasn't Young either!). Sometimes she would introduce her previous students to her current students. Other times they would just talk quietly at her desk and leave quickly. Either way, the meeting either began or ended with a warm embrace (sometimes both).

It was amazing to see a teacher so loved by her students! I wanted to be like her one day. I wonder what Mrs. Turner would think of my teaching career today :D

Ok, enough reminiscing! What brought on this trip to the past? This week, Teachers Pay Teachers is having a sitewide sale to honor the teacher heroes among us! My store, as well as many others, will be discounted to 20% OFF and then TPT throws on an extra 10% savings at checkout! (Just don't forget to type in the promo code: HEROES

Comment on this post with the item you are moving from your wishlist to your shopping cart, and I'll randomly select one commenter to win another item of equal value from my store. (Disclaimer, to qualify, your wish list item must be from my store. I can't give bonuses on other people's resources!)

Here are a few more teacher bloggers,

An InLinkz Link-up

Interactive Test Prep: Using Games to Review

Preparing for tests is rarely fun, at least from my school experience. What are some strategies you use to help your students prepare for tests, and not be bored out of their minds?





I love to use games, the most kids play the less they feel like they're learning. We all know that, but it's often hard to implement in traditional learning environments. Let's go back to the basics. What are the building blocks, or the foundations, of games used for review?

• We have whole class, or large group games, usually involve teams and some sort of competition. 
• Small group games of 2-5 players, maybe as many as 7 or 8. These games are typically a board game or card game. There is some goal to reach, and players usually compete to achieve the goal first. 
• Then we have individual games, this usually includes some form of puzzle, such as a cross word, a physical puzzle, a riddle or cryptogram, or something similar. 

When planning your test prep, it's important to know which of these platforms will serve your purpose the best. Once you've identified the platform, then it's time to figure out the specifics. The options for each game platform are innumerable.  

You might find an electronic game such as an interactive PowerPoint game the entire class will enjoy. These are usually very specific in content, but you can do your homework to find editable versions, or get creative and use a template to make your own. Here's a little lesson on using macros that might help ;) Most of the electronic apps and games we use for content review are based on typical physical games, such as Wheel of Fortune or Jeopardy. There are printed versions of these games as well that might be more suitable for your class/content. 

Other classroom games that have been popular for years are various races, Trivia Pursuit, Around the World, hangman (or other less gruesome versions), and so on. These are quick and easy to put into practice, because the only prep you need is your list of questions and a few simple rules on the board. 

The smaller games, board games and card games, this is my favorite. Breaking things down into smaller bits always seems to help students cement those skills and that knowledge. Working in a smaller group allows more of the students to participate, and each student usually has the opportunity to answer more frequently. I love cooperative games such as Memory, Wild (UNO), Go Fish, and Old Maid. 

Over the past 2 years, I've been building my supply of games that would help my students. SOme are just spin offs of popular games I mentioned, others, I like to think, I came up with the ideas. Although, the longer I"m around, the less I believe anyone has a truly unique idea anymore! Here are just a few of my most recent games that work well for reviewing, or building skills.

 

This same format is available with content for covering a unit on organisms, cells, or living systems. More are in the works that will include interdependence of life, adaptation and change, genetics, history of life on earth, and science investigations. 

I designed this for older kids who had been struggling with time for years. Because of their special learning abilities, they had never received actually teaching on telling time, elapsed time, or even the basics. This game really helped them understand what each part of the digital time represented and how that translates to words and the analog clock. 

This one was a lot of fun to make and play. My 6th graders still like to pull this one out and practice. I also made a few worksheets to go along with this. Even though I'm not a big fan of worksheets, it is nice to leave a few with my students when I won't be seeing them for a few days, just to know they'll be getting some practice in that I can assess later!

What about you? Do you have a few favorite games you like to use to review skills or concepts before a test? Feel free to add up to 3 links in the linky below, or post the concepts of the game in the comments. Thanks for stopping by!

An InLinkz Link-up