The first thing I always tell parents is that I believe some people aren't really capable of memorizing facts. I know this sounds like I'm saying they can't learn, it's is not the same thing I promise. But rote memorization really truly does not work for some people and has been the cause of frustration in the mathematics classroom for years. I have a firm belief that some math students will need to develop strategies and habits, which will help them retrieve information stored in their brain. This might include using fingers, counting objects in the room, or visualizing dots in their minds. Guess what? Their math teachers and tutors at times count on their fingers, look at concrete objects, and/or visualize patterns to solve problems as well!
1. Use the distributive Property.
The distributive property is one of the basic laws of how numbers work with each other. It works with both addition and multiplication, and helps students break down larger facts into more bite-sized facts that are easier to solve. The reason this strategy works well is it is not a trick, it's a law of numbers. It helps math students break apart numbers and use their values to find related facts they've already memorized or effectively stored for retrieval. The distributive property of multiplication basically states that numbers can be spread out to be multiplied and added to make an operation easier to solve.
Here is an example. Let's multiply 3 x 6. I'm starting off with a seemingly simple fact so it's easy to see how this works.

My student says, "Miss Stefany, I don't know my sixes!"
"Ok, what about your threes?"
My student, "No, I don't know my threes either!"
"No problem, do you remember how to count by 2s?"
My student, "Yes, 2, 4, 6, 8..."
"Perfect!"
Now you're asking, "How on earth is counting by 2s going to help me multiply 3 and 6?"
For that answer we need to go back to our basic addition facts. 6 is equal 2 + 4, correct? The distributive property of multiplication tells us that if 2+4=6 then 3x6=(3x2)+(3x4).

If you count the blocks in the diagram, you'll see that it works. There are 18 blocks in the 3 by 6 grid and there are 18 blocks in the 3 by 2 and 3 by 4 grid as well!
Maybe your student doesn't know his fours yet either. No problem, just break it down a further step. If 6=2+4 it also equals 2+2+2. So 3x6 also equals (3x2)+(3+2)+(3x2).
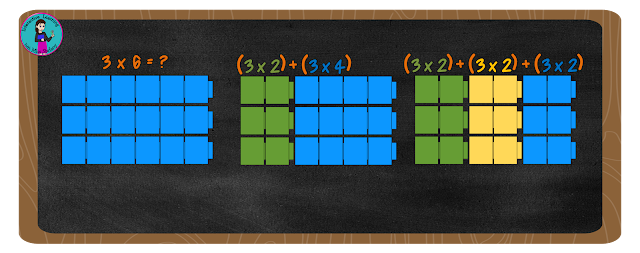
Again, counting the blocks shows that it works! And I can assure you, it works every time, no matter what the numbers are or how big they are.
You can also break the numbers down into any of their equal parts.
For example, 6=1+5, so 3x6=(3x1)+(3x5)
6=3+3, so 3x6=(3x3)+(3x3)
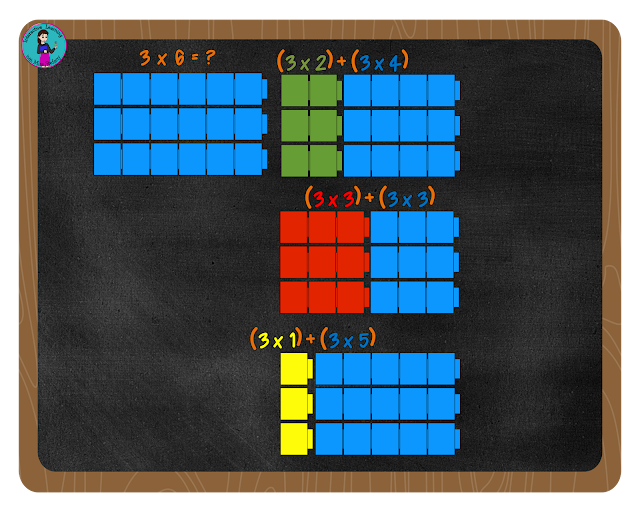
Just a tidbit here. If you your child was among those learning all the partners of numbers over the past 3 years with their Common Core Curriculum, and you couldn't figure out what they would ever do with that. Here it is! Be thankful they spent so much time with that concept, because now this will make so much more sense. If your child wasn't one of the students drilled on this skill, then see this post here for more information that might make using this strategy a little more clear.
Would you like to try some multiplication problems using this strategy with answer guide to check your work? Here's a freebie just for parents!



